러닝머신 하는 K-공대생
Graph-Cut 을 이용한 영상 분할 구현 본문
Ⅰ. 글을 시작하며
전에 최적화 분야를 공부하기 위해 ‘영상 이해를 위한 최적화 기법’강의를 듣던 중 영상 분할과 관련된 내용이 있었다. 영상 분할은 이미지를 여러 개의 픽셀 집합으로 나누는 것으로 컴퓨터 비전에서 중요한 주제다. 에너지 함수를 가지고 variational한 방법으로 최적화를 진행하거나 조합적 방법으로 그래프 컷에 기반하여 물체/배경 으로의 영상 분할을 진행하는 아이디어를 얻을 수 있었고 특히 그래프 컷을 활용해 영상 분할을 하는 아이디어가 흥미로웠다. 이에 영상 분할에 대한 최적화 방법들을 정리하고 관련 알고리즘을 학습하며 아이디어를 구체화시켜 밑바닥부터 직접 구현해 실제로 이미지를 주었을 때 영상 분할을 진행할 수 있는 프로젝트를 진행했었다. 나중에 정리해야지 미루고 있었는데 입시가 끝난 지금 내용을 정리해서 여러분들이 이 글을 통해 영상 분할에 대한 새로운 접근법에 대해 알아갔으면 좋겠다.
Ⅱ. 이론적 배경
2.1. 영상 분할
영상 분할은 의료영상, 위성 영상, 얼굴 인식 등에 실용적으로 활용된다. 컴퓨터 시각에서 분할은 영상을 여러개의 픽셀 집합으로 나누는 과정을 의미하며 영상 분할은 영상에서 물체와 경계를 찾는데 사용된다.
2.2 combinational optimization (조합 최적화)
조합 최적화의 영역은 feasible set이 이산 집합에 속하거나 이산적인 것으로 변환될 수 있고, 가장 좋은 해를 찾는 것이 목적인 최적화 문제이다. 연속적 집합에서 정의한 비용함수를 이산적으로 정의해서 문제를 풀어가는 본 탐구의 방법이 조합 최적화 방법이다.
2.3. 유량 네트워크
각 간선에 용량(capacity)란 추가 속성이 존재하는 방향 그리프로 각 간선은 유량을 흘려보내는 역할을 한다. 용량 제한 속성과 유량의 대칭성, 유량의 보존 속성을 만족해야 하며 각 간선이 용량을 갖는 그래프에서 두 source에서 sink로 얼마나 많은 유량을 보낼 수 있는지 계산하는 문제를 네트워크 유량 문제로 부른다.
Ⅲ. 이론 분석 및 구현
1. Energy based Image Segmentation 분석
조합 최적화 방법을 얘기하기 전에 variational 한 방법을 소개하겠다. 에너지 함수를 기반으로 영역 분할을 진행하는 variational한 방법들로 컨투어를 잡거나 level set을 이용하는 방법을 주로 사용한다.
1.1. Snake Algorithm : Active Contour Models


경사하강법을 이용해 업데이트 하는 것 외로도 variational calculus와 Euler-Lagrange 미분 방정식을 이용하면,
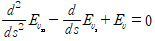

1.2. Level-set method
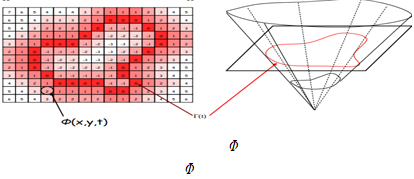
1.1 에서의 방법에서는 곡선 위의 점들을 정의해 이동시켜 컨투어를 찾는 방법으로 분할을 진행했지만 다양한 위상적 변화를 다루는데 한계가 있다. Φ 라는 면을 정의해 c에서의 level-set과 Φ가 만나서 생기는 곡선 $(x, y) | Φ(x, y) = c$ 을 경계로 컨투어를 잡고 영역분할을 진행한다. 마찬가지로 energy functional을 최소화하도록 기울기를 이용해 t에 따른 Φ 를 업데이트 하여 컨투어를 찾는다.
2. Graph Cut based Image Segmentation 분석
앞의 영상 분할을 위한 variational 방법론에선 연속적인 도메인에서 에너지 함수를 정의하여 최적화하는 방식으로 진행했지만 결국 컴퓨터는 이산적으로 값을 처리하기에 수치적 방법을 사용해서 처리하기에 같은 에너지 함수라도 구현 방식에 따라 영상 분할의 결과가 달라질 수 있다. 그래서 시작부터 이산적으로 에너지 함수를 정의하여 조합 최적화 방식으로 문제를 해결하는 방법론이 등장했다.
2.1. 이산 비용함수와 영상 분할
$A=(A _{1} ,A _{2} ,...,A _{|P|} )$ 를 각 픽셀들이 물체(obj)인지 배경(bkg)인지 정보를 담고 이진 벡터라고 하면 비용함수 $E(A) = \lambda R(A)+B(A)$ 로 두고 이때 $R(A) = \sum _{p \in P} ^{} R _{p} (A _{p} ) (regional term)$, $B(A) = \sum _{(p,q) \in N} ^{} B _{p,q} \cdot \delta _{A _{p} != A _{q}} (boundary term)$ 로 이산적으로 비용함수를 정의할 수 있다. regional cost는 각각에 픽셀에 대해 $R _{p} (obj)=-lnPr(I _{P} | obj)$ 이나 $R _{p} (obj)=-lnPr(I _{P} | bkg)$ 로 현재 A에 대해 각 픽셀의 값이 적당한지를 나타내는 조건부 확률에 –ln 를 씌워 적절히 예측했으면 0에 가깝게 되고 적절하지 않으면 값이 커지게 된다. boundary cost에서 $B_{p, q} \propto exp(- {{I_p - I_q}^2 \over 2 \sigma ^2}) \cdot {1 \over dist(p,q)} $ 이고 인접한 두 픽셀 p, q가 비슷한 값을 가지면 $B_{p,q}$ 값이 커지고 둘이 많이 차이날 때 값이 작아진다. $\delta _{A _{p} != A _{q}}$ 가 $A_p = A_q$ 일 때 0, $A_p != A_q$ 일 때 1인 점을 고려하면 다른 클래스로 예측할 때 값의 차이가 클 것이라는 예상에 부응하여 적절한 이산 비용함수임을 알 수 있다. 그리고 비용함수를 최소화하는 $A$를 구하게 되면 영역 분할을 진행할 수 있다.
2.2. Graph cut으로 구하는 최적해
픽셀 개수가 P개 일 때 모든 경우 $2^P$번 모든 경우를 찾는 것은 시간적으로 불가능하므로 다른 효과적인 방법이 필요하다.“Graph Cuts and Efficient N-D Image Segmentation”를 참고하면$ V=P \cup \{S,T\}, G = (V, E)$ 으로 Object 터미널을 지나 각 픽셀들을 지나고 Background 터미널로 흐르는 유량 그래프를 그림 3의 왼쪽과 같이 구성하고 각 간선의 비용을 그림4와 같이 설정했을 때 이 유량 그래프의 최소 컷이 1.1에서의 비용함수를 최소화을 보일 수 있고 증명은 생략하겠다.

이 최소컷으로 나뉘어진 2개의 그룹들은 각각 배경과 물체 중 하나이므로 graph cut을 이용한 영상 분할을 진행하기 위해선 입력받은 이미지를 source와 픽셀들, sink로 연결된 유량 그래프로 나타내어 배경과 물체에 대한 정보를 입력받고, 적절히 비용함수를 계산해 간선에 가중치를 부여하고 최소컷 알고리즘을 이용하여 적절히 2개의 집합으로 나누어야 한다. 구현해야할 부분이 많아 클래스로 묶어 모듈화시켜 간단하게 사용할 수 있도록 할 필요가 있다.
3. 이미지 입력 및 물체/배경 정보
이미지를 입력받고 각 픽셀값과 물체(obj)와 배경(bkg)에 대한 사용자 라벨 정보, regional cost를 얼마나 고려할지를 결정하는 alpha (앞 수식에서 lambda)를 객체 생성할 때 입력 받는다. alpha값이 클수록 regional cost의 가중치가 커져 사용자 라벨과 픽셀값의 유사성의 중요도가 커지게 된다.
class Segmentation:
def __init__(self, img: np.ndarray, objLabel, bkgLabel,alpha):
self.img = img
self.bkg = bkgLabel
self.obj = objLabel
self.alpha = alpha4. 비용 함수 구현
4.1. Boundary Cost
이웃한 픽셀은 상하좌우 4방향만 따질 것이므로 $B_{p, q} \propto exp(- {{I_p - I_q}^2 \over 2 \sigma ^2}) \cdot {1 \over dist(p,q)} $ 에서 dist(p,q)는 1로 두었고 비용함수가 너무 작아지는 것을 방지하기 위해 100을 곱하고 적절히 $\sigma = 30$ 로 두었다.
def B(self, p, q):
return 100 * exp(-pow(int(p) - int(q), 2) / (2 * pow(30, 2)))4.2. Regional Cost
현재 픽셀값이 배경에 가까운지 물체에 가까운지 $R_p(obj) = -lnPr(I_p|obj)$ 를 계산하기 위해 $Pr(I_p|obj)$ 를 구해야 했다. 물체와 배경 라벨 정보를 활용하고자 했고 히스토그램 분석을 통해 그림 5의 (a)와(b)처럼 물체와 배경 각각에 대해 가우시안 분포를 계산하여 $Pr(I_p|obj)$ 와 $Pr(I_p|bkg)$ 를 얻을 수 있었다. 이를 통해 $R_p(obj), R_p(bkg)$ 를 반환하는 함수를 만들었다.
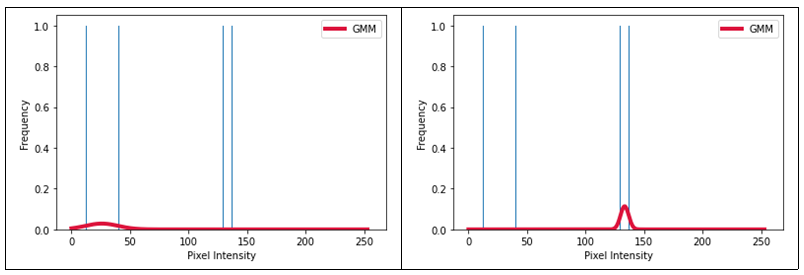
def get_gmm(self):
bkg_values = [self.img[i[0]][i[1]] for i in self.bkg]
obj_values = [self.img[i[0]][i[1]] for i in self.obj]
hkg_hist, _ = np.histogram(bkg_values, 256, [0, 256])
obj_hist, _ = np.histogram(obj_values, 256, [0, 256])
obj_gmm = GaussianMixture(n_components=1)
obj_gmm = obj_gmm.fit(X=np.expand_dims(obj_values, 1))
bkg_gmm = GaussianMixture(n_components=1)
bkg_gmm = bkg_gmm.fit(X=np.expand_dims(bkg_values, 1))
return obj_gmm, bkg_gmm
def R(self, p, obj_gmm, bkg_gmm):
p_obj = np.exp(obj_gmm.score_samples([[p]]))
p_bkg = np.exp(bkg_gmm.score_samples([[p]]))
p_p_obj = p_obj / (p_obj + p_bkg)
p_p_bkg = p_bkg / (p_obj + p_bkg)
return -np.log(p_p_obj), -np.log(p_p_bkg)5. 그래프 생성
이미지의 노드 개수에 source와 sink를 더해 그래프 노드 수 V를 계산하고 VxV 행렬로 인접행렬 방식으로 그래프를 초기화한다. 사용자가 준 라벨 정보가 정확하다고 가정해 K는 매우 크게 설정하였다.
- Regional Cost 할당:
dsource와 픽셀 p, p와 sink 가 연결되어 있는 간선의 가중치를 설정하는 부분으로 4에서 구한 비용함수와 라벨이 배경인지 물체인지에 따라 경우를 나눠 그림 4와 같이 할당해주고 source -> p -> sink 쪽으로 방향성을 고려하였다.
- Boundary Cost 할당:
현재 픽셀 p에서 상하좌우 4방향으로 인접해있는 픽셀들에 대해 boundary cost $B_{p,q}$ 를 계산하고 양방향 간선으로 이어주었다.
def make_graph(self):
r, c = self.img.shape
V = r * c + 2
G = np.zeros((V,V))
K = 1e9
# Regional Cost
obj_gmm, bkg_gmm = self.get_gmm()
for i in range(r):
for j in range(c):
if (i, j) in self.obj:
G[0][1 + c * i + j] = K
G[1 + c * i + j][V - 1] = 0
elif (i, j) in self.bkg:
G[0][1 + c * i + j] = 0
G[1 + c * i + j][V - 1] = K
else:
R_bkg, R_obj = self.R(self.img[i][j], obj_gmm, bkg_gmm)
G[0][1 + c * i + j] = self.alpha * R_obj
G[1 + c * i + j][V - 1] = self.alpha * R_bkg
# Boundary Cost
for i in range(r):
for j in range(c):
if i - 1 >= 0 and G[c * i + j + 1][c * (i - 1) + j + 1] == 0:
G[c * i + j + 1][c * (i - 1) + j + 1] = self.B(self.img[i][j], self.img[i - 1][j])
G[c * (i - 1) + j + 1][c * i + j + 1] = self.B(self.img[i][j], self.img[i - 1][j])
if i + 1 < r and G[c * i + j + 1][c * (i + 1) + j + 1] == 0:
G[c * i + j + 1][c * (i + 1) + j + 1] = self.B(self.img[i][j], self.img[i + 1][j])
G[c * (i + 1) + j + 1][c * i + j + 1] = self.B(self.img[i][j], self.img[i + 1][j])
if j - 1 >= 0 and G[c * i + j + 1][c * i + (j - 1) + 1] == 0:
G[c * i + j + 1][c * i + (j - 1) + 1] = self.B(self.img[i][j], self.img[i][j - 1])
G[c * i + (j - 1) + 1][c * i + j + 1] = self.B(self.img[i][j], self.img[i][j - 1])
if j + 1 < c and G[c * i + (j + 1) + 1][c * i + (j + 1) + 1] == 0:
G[c * i + j + 1][c * i + (j + 1) + 1] = self.B(self.img[i][j + 1], self.img[i][j])
G[c * i + (j + 1) + 1][c * i + j + 1] = self.B(self.img[i][j + 1], self.img[i][j])
return G
6. 최소 컷 구현 및 영상 분할
최대 유량은 최소컷의 용량과 같다는 max-flow/min-cut 이론에 근거해 최소컷은 네트워크의 최대유량을 구하는 Ford-Fulkerson 알고리즘을 활용하여 구현하였다.
BFS로 경로를 탐색하고 잔여 용량이 남아있는 간선을 탐색하여 증가 가능 경로가 없으면 종료해 증가 경로를 통해 얼마나 보낼지를 결정하고 증가 경로로 유량을 보내었다. 이때 유량의 대칭성을 이용해 역방향 간선을 다루어 최적해를 찾을 수 있게 최대 유량 알고리즘 구현을 진행하였다.
def networkFlow(self, source, sink, capacity, flow):
N, totalflow = len(capacity), 0
while True:
parent = [-1] * N
queue = deque()
parent[source] = source
queue.append(source)
while queue and parent[sink] == -1:
p = queue.popleft()
for q in range(N):
if capacity[p][q] - flow[p][q] > 0 and parent[q] == -1:
queue.append(q)
parent[q] = p
if parent[sink] == -1: break
p, amount = sink, int(1e9)
while (p != source):
amount = min(amount, capacity[parent[p]][p] - flow[parent[p]][p])
p = parent[p]
p = sink
while (p != source):
flow[parent[p]][p] += amount
flow[p][parent[p]] -= amount
p = parent[p]
totalflow += amount
return totalflow
ford-fulkerson 알고리즘만으론 네트워크의 최대 유량, 즉 앞서 설정한 비용함수의 최소값만 알 수 있으므로 어떤 간선을 제거했는지 알아야 영상 분할이 가능하다. 유량과 용량이 같은 컷이 최소 컷이므로 capacity를 저장하는 그래프 G, ford-fulkerson 알고리즘을 적용하면서 유량을 저장하는 F에서 G에서의 용량과 F에서의 흐름이 0이 아닌 같은 값을 가지는 간선을 제거하면 된다. 즉 source 에서부터 dfs로 이동하면서 용량과 흐름이 같은 간선들을 끊어주고 다시 source에서부터 dfs를 진행해 이동가능한 정점들은 object로 이동 불가능한 정점들은 background로 나타내어 object 영역 mask을 추출하였다.
다음은 G,F를 초기화하고 최대 유량 알고리즘을 적용해 dfs로 최소컷을 구현하는 과정과 source에서 dfs를 진행해 이동가능한 정점만 object로 마스킹하는 과정을 구현한 것이다.
def run(self):
r, c = self.img.shape
V = r * c + 2
G = self.make_graph()
F = np.zeros((V, V))
self.networkFlow(0, V - 1, G, F)
def dfs(graph, s, visited):
visited[s] = True
for i in range(len(graph)):
if graph[s][i] > 0 and not visited[i]:
dfs(graph, i, visited)
visited = [False] * V
dfs(G, 0, visited)
for i in range(V):
for j in range(V):
if visited[i] and G[i][j] == F[i][j] != 0:
G[i][j] = 0
group = [False] * V
dfs(G, 0, group)
mask = np.zeros((r, c))
for i in range(r):
for j in range(c):
if group[1 + i * c + j]:
mask[i][j] = 1
return maskⅣ. 결과
위에서 설명한 것 처럼 각 과정을 Segmentation 클래스로 묶어서 모듈화시켰고 아래와 같이 이미지와 라벨 힌트를 인자로 받아 인스턴스를 생성해 구현한 graph-cut 기반 영상 분할을 진행한 mask를 반환하도록 하였다.
처음엔 간단하게 3x3 이미지를 생성하고 라벨 힌트를 주어서 기본적으로 구현한 알고리즘이 잘 작동하나 확인해보았다. 그림 6,7에서 왼쪽이 원본 이미지고 오른쪽이 영상 분할된 결과 이미지이다. 라벨 힌트를 주었을 때 올바르게 분할이 진행됨을 알 수 있다. 상황이 단순하여 이외 대부분의 경우에도 정확하게 분할이 진행된 것으로 기본적으로 알고리즘이 잘 구현되었음을 확인할 수 있다.


좀 더 복잡한 상황을 보기위해 Berkeley Segmentation Dataset 내 이미지에 대해서 적용하고자 했고 구현한 최대 유량 알고리즘의 시간복잡도가 $O(VE^2)이라서 20x20 흑백 이미지로 단순화하여 물체와 배경 내에서 대략 직선으로 라벨 힌트를 주고 영상 분할을 진행해보았다.

그림 8에서 요트만을 검출하고 싶었지만 배경에서도 비슷한 픽셀값을 가진 경우에도 물체로 분할이 되는 문제가 발생하였다. alpha 값을 기존 1에서 0.5, 0.1로도 진행하여 초기 사용자가 정한 라벨의 픽셀값의 의존도를 낮춰보았다. 그림 9에서 볼 수 있듯이 3번째 경우 (alpha=0.1) 일 때 물체 부분만 정확히 추출할 수 있었다

다른 경우에도 성립하는지 확인해보았다. 그림 10에서와 같이 물체를 (10,10),(11,10),(12,10),(13,10), 배경을 (5,7)부터 (5,15)까지 이은 직선으로 라벨정보를 주었을 때 alpha를 1, 0.1일 때 각각 영상 분할을 진행해보았다. alpha가 1일때는 사용자가 물체라고 표시한 부분만 물체로 인식하였으나 alpha가 0.1일 때는 그 주변 유사한 픽셀들까지 물체로 정하여 물체를 제대로 인식하였다.

사실 alpha 값보다는 사용자의 라벨 정보 또한 영상 분할의 결과에 많은 영향을 미친 것 같. 그림 11의 영상 분할 결과 1에서는 obj = [(i,15) for i in range(15,20)], bkg = [(i,5) for i in range(10,20)] 로 라벨 힌트를 주었고 성의 전체 영역을 추출하기를 기대했지만 픽셀값이 유사한 부분만을 물체로 인식하였다. 물론 25x25 이미지 내에서만 본다면 합리적인 영역 분할이지만 왼쪽에 그림자 때문에 픽셀값이 다른 부분도 물체로 주려고 (15,13)에서 (20,13)까지 이은 직선이 물체라는 정보를 추가하여 영상 분할 결과 2를 얻었고 적절하게 성의 벽면을 모두 물체로 마스킹하였다.

Ⅴ. 결론 및 제언
정리하자면 영역 분할을 variational optimization, combination optimization 방법으로 풀어내는 방법에 대해 분석하고 최대 유량 알고리즘, 최소 컷 등의 그래프 이론에 대해 학습하여 직접 구현 아이디어를 세워 Graph-Cut을 이용한 영상 분할 프로그램 구현을 진행하였고 작은 사이즈에 이미지와 적절한 라벨 힌트 내에서 만족할만한 영상 분할 결과를 얻을 수 있었다. 좀 더 일반적인 이미지 사이즈에 적용시키기 위해 최소 컷을 구현한 부분에서 효율적으로 작동할 수 있게 알고리즘을 수정할 필요가 있다. 또한 직접 물체/배경 정보를 입력받도록 했지만 GUI 툴을 만들어 라벨 정보를 쉽게 입력받을 수 있도록 발전시키고 싶다. 사실 최대 유량 알고리즘을 개선해도 극적으로 빨라지길 기대하긴 힘들어 보인다. 이미지 픽셀 자체를 그래프의 정점으로 두어 너무 많은 정점과 간선이 발생한다는 점에 집중해 각 픽셀 자체를 정점으로 하기보다 계산량을 줄이기 위해 특성이 유사한 픽셀들을 군집화해 하나의 그룹으로 만드는 슈퍼픽셀을 이용하여 그래프를 구성한다면 빠른 시간과 적은 연산량으로 유량 알고리즘을 적용할 수 있을 것이다.
+ 이 프로젝트에 사용된 소스코드와 저장된 노트북: https://github.com/taegukang35/graphcut_segmentation
GitHub - taegukang35/graphcut_segmentation
Contribute to taegukang35/graphcut_segmentation development by creating an account on GitHub.
github.com
■ 참고 문헌
[1] Y. Boykov and G. Funka-Lea, “Graph Cuts and Efficient N-DImage Segmentation,” IJCV 70(2), 109-131, 2006.
[2] https://nuguziii.github.io/survey/S-002/
[4] https://kooc.kaist.ac.kr/optimization2017/joinLectures/9701
[5] https://en.wikipedia.org/wiki/Maximum_flow_problem
[6] https://en.wikipedia.org/wiki/Ford%E2%80%93Fulkerson_algorithm
[7] https://en.wikipedia.org/wiki/Max-flow_min-cut_theorem
'Project' 카테고리의 다른 글
| 내가 과학고에서 뭐했더라 (0) | 2022.07.21 |
|---|---|
| TOBDA App 개발 근황 (2) | 2021.09.23 |
| 톺다(TOBDA), 시각장애인의 진정한 독립보행을 돕다 (0) | 2021.08.10 |
| 두 과고생의 뜨거운 도전, 2020 캔위성 경연대회 (2) | 2021.04.03 |




