러닝머신 하는 K-공대생
12865번: 평범한 배낭 (DP 테이블) 본문
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
일단 DP로 풀 수 있을 것 같아서 점화식부터 세우려고 시도했다. D(i,k)를 i번째 인덱스 이후 중, k이하의 무게 중 가치의 합의 최댓값 으로 두고서 생각을 했다. 보통 조합론적 증명을 할 때 처럼 자신을 포함시킬 때와 포함하지 않을 때 경우를 나누어 V[i] 를 i번째 인덱스의 가치, W[i]를 i번째 인덱스의 무게라고 했을 때 i번째와 i+1번째 관계를 이끌어냈다.

일단 점화식을 유도하긴 했는데 어떻게 써먹을 수 있을지 고민하다, D(i,k)를 구하기 위해서는 D(i+1,k-W[i])와 D(i+1,k)가 필요해서 D(i,k)를 저장하는 DP 테이블을 만들고 차례대로 채워넣어서 문제에서 입력으로 준 n,k 즉 D(n,k)를 만들고자 했다. DP 테이블의 가로축은 0~k 까지의 무게를 나타내었고 세로축은 인덱스를 넣어 D(i,j)를 i번째 인덱스 이후 중, j이하의 무게 중 가치의 합의 최댓값을 DP 테이블의 값으로 넣었다.
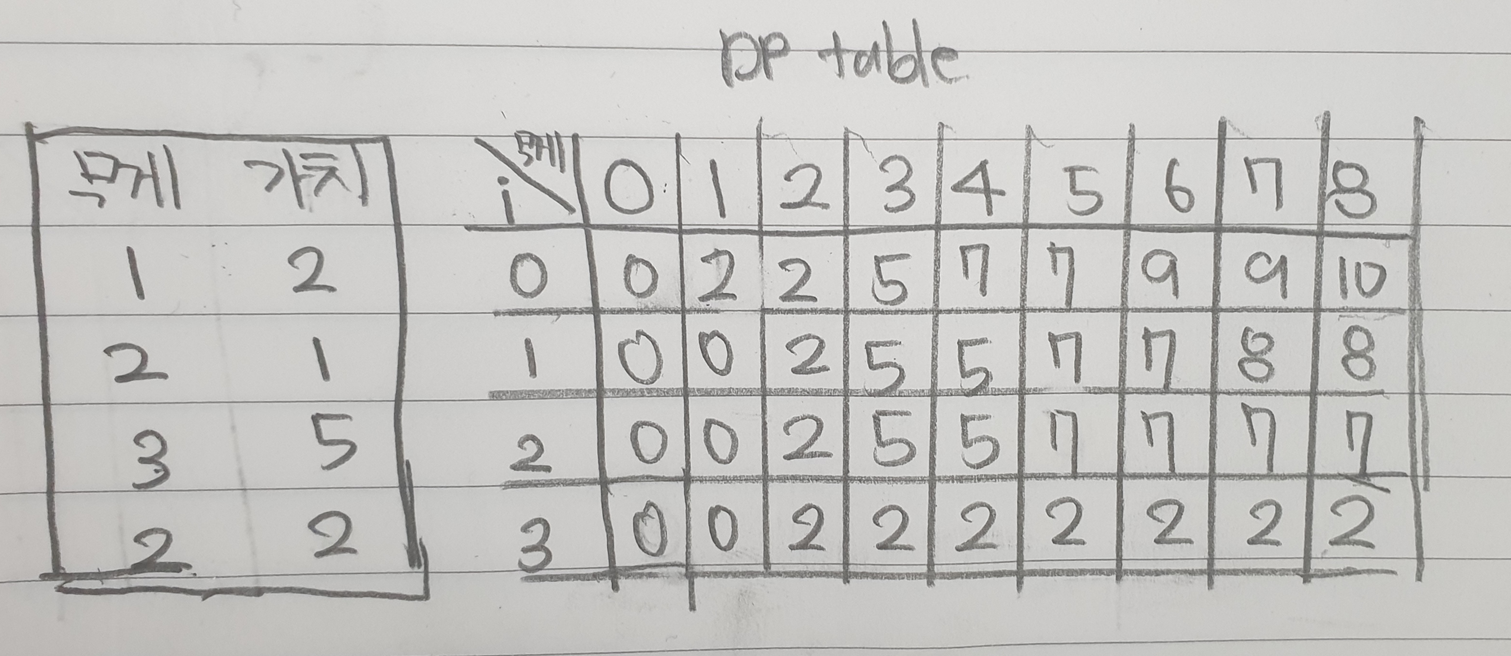
예를 들어 무게가 8이하인 경우 다음과 같이 인덱스에 따른 무게 W, 가치 V가 있고 빈 DP 테이블이 있을 때,

3번째 인덱스부터 DP table을 채워넣자. 이때 W[3] 보다 무게가 작은 경우 0으로 두었다.

2번째 인덱스에서는 유도한 수식을 통해 DP 테이블을 채워넣고, W[2] 보다 무게가 작은 경우 0이 아닌 다음 인덱스에 있는 값을 넣어 D(i,j)의 의미인 'i번째 인덱스 이후 j이하의 무게 중 가치의 최댓값'을 보존한다.

마찬가지로 1번째, 0번째 인덱스도 순서대로 채워넣는다. 그리고 가치합의 최댓값은 정의상 D[0][8]이 된다.
방금 예시를 통해 직접 DP 테이블을 채우는 순서와 규칙대로 코드를 작성했다.
- 마지막 인덱스부터 0번째 인덱스 순으로 DP 테이블을 채운다.
- 마지막 인덱스일 경우 DP table을 채울 때 마지막 인덱스의 무게보다 작을 때는 0을 채워넣고 마지막 인덱스의 무게 이상일때는 마지막 인덱스의 가치를 채워넣는다. (D[i][j] 정의상 당연함)
- D(i+1,j-W[i])의 값이 존재하지 않을 때, 즉 i번째 인덱스의 무게보다 작을 때는 i+1번째 DP table 값을 넣음
- D(i+1,j-W[i])의 값이 존재할 때, 위에서 구한 점화식대로 DP 테이블을 채워넣는다.

n,k = map(int,input().split())
V = []
W = []
for i in range(n):
a,b = map(int,input().split())
W.append(a)
V.append(b)
dp = [[0 for i in range(k+1)] for j in range(n)]
for i in range(n-1,-1,-1):
for j in range(k+1):
if i == n-1:
if j-W[i]>=0:
dp[i][j] = V[i]
continue
if j-W[i] < 0:
dp[i][j] = dp[i+1][j]
continue
dp[i][j] = max(dp[i+1][j-W[i]] + V[i], dp[i+1][j])
print(dp[0][k])'Problem Solving > BOJ' 카테고리의 다른 글
| 1007번 : 벡터 매칭 (브루트포스, 조합) (0) | 2021.08.10 |
|---|---|
| 1655번: 가운데를 말해요 (우선순위 큐) (1) | 2021.02.15 |
| 1654번: 랜선 자르기 (이진 탐색) (1) | 2021.02.15 |
| 16929번: Two Dots (DFS, 사이클 판단) (0) | 2021.02.15 |
| 1103번: 게임 (DFS, 메모이제이션) (0) | 2021.02.12 |




