러닝머신 하는 K-공대생
1007번 : 벡터 매칭 (브루트포스, 조합) 본문
1007번: 벡터 매칭
평면 상에 N개의 점이 찍혀있고, 그 점을 집합 P라고 하자. 집합 P의 벡터 매칭은 벡터의 집합인데, 모든 벡터는 집합 P의 한 점에서 시작해서, 또 다른 점에서 끝나는 벡터의 집합이다. 또, P에 속
www.acmicpc.net
Abstract:
오늘 벡터 문제를 풀다가 집에 와서 백준에 벡터 관련된 문제가 없을까 풀어보았다. 벡터 정의만 알면 돼서 아이디어 떠올리는 것은 쉽고 어떻게 구현할지 고민을 많이 했다. 고민하다 백트래킹으로 조합을 계산했고 추가적으로 파이썬 내장 라이브러리인 itertools의 combination 함수를 이용하여 편하게 풀었다.
문제 접근 및 해설:
문제에서 중요한 것은 P에 속하는 모든 점은 한 번씩 쓰여야 하므로 각 벡터의 시작점과 끝점은 다른 벡터와 공유하면 안 된다. 두 점 A, B를 잇는 벡터를 구하려면 벡터의 연산을 알아야 한다. 주어진 좌표가 좌표명면 위 원점을 시작점으로 하는 공간벡터를 나타낸다고 생각하면 $\overrightarrow{OA},\overrightarrow{OB}$ 에 대해 $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$ 가 성립한다. 이때 우리는 이 벡터들의 합만 계산하면 되므로 $\sum \overrightarrow{B_{i}A}_{i}=\sum \overrightarrow{OA}_{i}-\sum \overrightarrow{OB}_{i}\\$ 가 성립하고 P에 속하는 점 중 $\overrightarrow{OA}$ 처럼 더할 점과 $\overrightarrow{OB}$ 처럼 뺄 벡터에 대응되는 점들을 각각 n/2 개식 찾아주면 된다. 이 n/2개의 점을 구해주기만 하면 되고 $n<=20$ 이므로 $\begin{pmatrix} n \\n/2 \end{pmatrix}$ 번 브루트포스하게 계산해서 최솟값을 구하면된다.(계산은 각 벡터의 성분을 다 더하고 나중에 2번 빼주면 된다) 즉, 입력으로 들어온 n개의 점 중 n/2개를 뽑는 모든 조합의 경우를 계산해야 한다.
- 방법1. 백트래킹
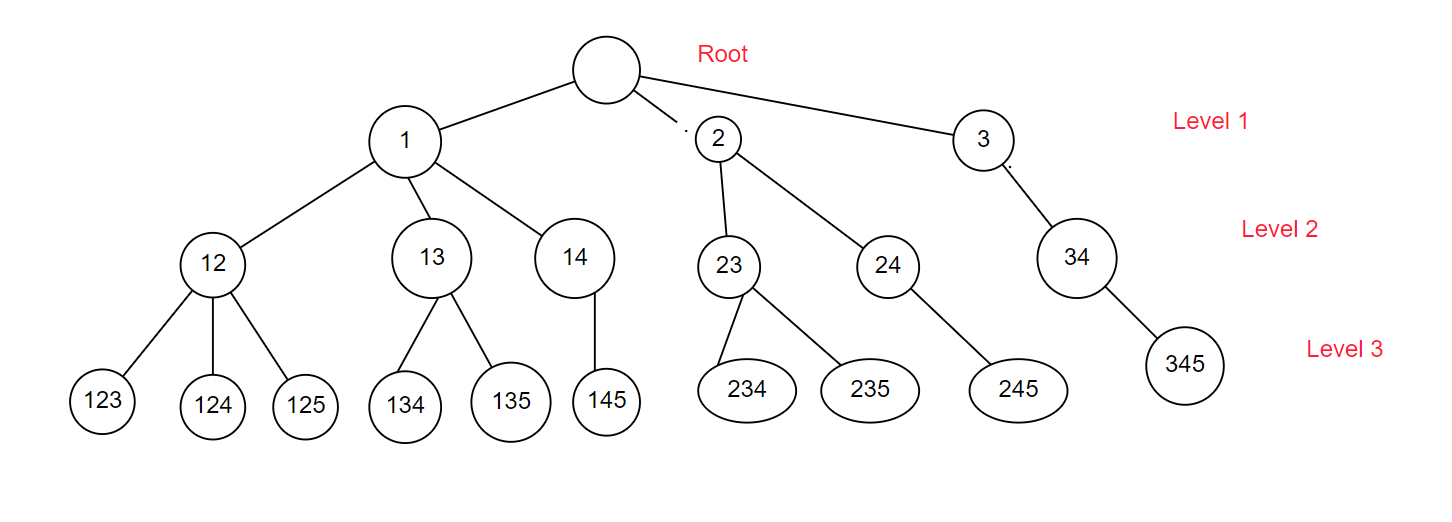
예를 들어 arr = [1,2,3,4,5]에서 $n(S)=3$ 인 집합 S를 뽑는 상황을 생각해보면 아래와 같이 상단 노드에서 시작해 트리를 구성해가면서 Level 3에 해당하는 노드들을 모두 얻어야 한다. 이는 재귀적으로 구할 수 있다.
arr = [i for i in range(5)]
n = len(arr)
l = 3
graph = [[] for i in range(n+1)]
for i in range(n+1):
for j in range(i+1,n+1):
graph[i].append(j)
def dfs(start,level,res):
if level == l:
print(res)
return
for i in graph[start]:
res[level] = i
dfs(i,level+1,res)
dfs(0,0,[0]*(l))
- 방법2. itertools 이용
itertools.combinations(iterable, r) 는 레퍼런스를 참고하면 아래와 같이 구성되어 있으며, iterable한 입력에 대해 조합을 계산하여 이 조합 튜플이 정렬된 순서로 생성된다.
def combinations(iterable, r):
# combinations('ABCD', 2) --> AB AC AD BC BD CD
# combinations(range(4), 3) --> 012 013 023 123
pool = tuple(iterable)
n = len(pool)
if r > n:
return
indices = list(range(r))
yield tuple(pool[i] for i in indices)
while True:
for i in reversed(range(r)):
if indices[i] != i + n - r:
break
else:
return
indices[i] += 1
for j in range(i+1, r):
indices[j] = indices[j-1] + 1
yield tuple(pool[i] for i in indices)
작성 코드(Python3):
1. 백트래킹

import sys
input = sys.stdin.readline
def solve():
n = int(input())
arr = []
x,y = 0,0
for i in range(n):
inp = list(map(int,input().split()))
arr.append(inp)
x+=inp[0]
y+=inp[1]
# 재귀적으로 combination 구하기
graph = [[] for i in range(n + 1)]
for i in range(1,n + 1):
for j in range(i + 1, n + 1):
graph[i].append(j)
# 루트 노드의 자식 노드를 제한하자
graph[0] = [i for i in range(1,n//2+2)]
brute = []
def dfs(start, level, res):
if level == n//2:
# brute.append(res)로 하면 brute안에 있는 모든 요소는 똑같은 리스트 res를 참조하므로
# res값이 바뀌면 brute의 요소들도 똑같이 바뀐다. 따라서 res[:]로 복사해서 넣어주자
brute.append(res[:])
return
for i in graph[start]:
res[level] = i
dfs(i, level + 1, res)
dfs(0, 0, [0]*(n//2))
# 브루트포스
ans = int(1e9)
for i in brute:
nx = x
ny = y
for j in i:
nx -= 2*arr[j-1][0]
ny -= 2*arr[j-1][1]
s = (nx**2+ny**2)**0.5
if s<ans:
ans = s
print(ans)
t = int(input())
for _ in range(t):
solve()2. itertools 라이브러리 이용

import sys
from itertools import combinations
input= sys.stdin.readline
def solve():
n = int(input())
arr = []
x,y = 0,0
for i in range(n):
inp = list(map(int,input().split()))
arr.append(inp)
x+=inp[0]
y+=inp[1]
ans = int(1e9)
for i in list(combinations([i for i in range(n)],n//2)):
nx = x
ny = y
for j in i:
nx -= 2*arr[j][0]
ny -= 2*arr[j][1]
s = (nx**2+ny**2)**0.5
if s<ans:
ans = s
print(ans)
t = int(input())
for _ in range(t):
solve()'Problem Solving > BOJ' 카테고리의 다른 글
| 1655번: 가운데를 말해요 (우선순위 큐) (1) | 2021.02.15 |
|---|---|
| 12865번: 평범한 배낭 (DP 테이블) (0) | 2021.02.15 |
| 1654번: 랜선 자르기 (이진 탐색) (1) | 2021.02.15 |
| 16929번: Two Dots (DFS, 사이클 판단) (0) | 2021.02.15 |
| 1103번: 게임 (DFS, 메모이제이션) (0) | 2021.02.12 |




